Introduction to Pente AI

-

Approximating Optimal Solutions to Massively Complex, Deterministic Games


What do Google Maps, many board games, and social media websites have in common?  These are a small subset of things that have parts that can be modeled as "graphs".  For anyone who is not familiar with computer science or discrete math lingo, the word "graph" here does not refer to a visualization or plot, but instead it refers to a collection of connected data points, where each data point is called a "node" and each connection between nodes is called an "edge".

For example, with Google Maps, nodes may represent road intersections and edges may represent the streets or highways connecting those intersections.  With a board game like Chess, though, the nodes may represent game states (i.e. a snapshot of where all pieces are at or before a player takes a turn) and the edges may be the moves taken to get from one game state to another.  With social media websites, the nodes in the graph may be users, and the edges may represent some sort of connection between users, whether that connection represents one user following another, or a user interacting with someone else's posts, or any other form of connection or interaction between two users.

Imagine you're visiting New York City, and you want to travel from your hotel to the nearest grocery store, but you don't know where the store is or the most efficient way to get there.  So you open Google Maps and ask it to give you directions, but it tries to route you from New York City to Dallas to San Francisco, through three small towns on the west coast, and back to the grocery store that was three blocks away from your hotel.  Obviously, this route is a terrible route, given that we want to minimize the time spent getting to the grocery store!

Let's generalize the issue.  We have some graph, and some optimization goal.  The goal could be to minimize travel time between two points (for travel planning), maximize the number of user interactions (for social media websites), or maximize the number of games won (when exploring the graph representation of a board game).  But the number of paths to choose from is unfathomably large, and we can't possibly explore all possible paths through the graph to find the set of paths that best achieves our goal, so we have to find some algorithm to make clever guesses about which path will best optimize our chosen goal.

We will explore this problem on a sort of toy example by working to train a neural network to play two player Pente by efficiently exploring the graph of possible game states.  Pente is much like TicTacToe, but the board is 19 by 19 instead of 3 by 3, and there can be two to four players.  The goal is to either get five pieces in a row or capture five pairs of opponents' pieces (see Figures 1 and 2 for demonstration of how capturing pairs does and does not work).  Much like the other types of graphs mentioned, the graph that represents game states and moves for Pente is much too large to completely explore given our current computing power limits, but the fact that Pente has simple rules makes the game easy to write a simulator for.


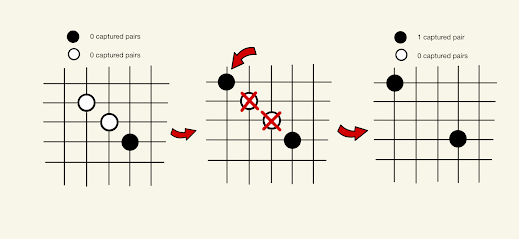Figure 1: Black captures one white pair


Figure 2: Black does not capture one white pair

Why is this project important, though?  Perhaps as you read this, you think that trying to create clever heuristics for playing a board game like Pente, Chess, Go, or other board games is simply an expression of eccentricity with no actual uses in the real world.  This could not be more wrong.  Better graph exploration methods (that are sometimes discovered or invented for fun purposes like making an AI to play Pente, Chess, or Go) are useful to make better internet search engines, music recommendations, self-driving cars, directions to the grocery store, and so many more uses.  Improving graph exploration methods directly impacts all of these aspects of normal people's everyday lives.

The following questions are particularly relevant:
  1. Is it currently computationally feasible for a college student with fairly limited computing power to replicate a simpler version of AlphaZero?
  2. Is there a better way than Monte Carlo Tree Search to balance exploration and exploitation for reinforcement learning in deterministic and discrete games?
  3. How large of a neural network is needed to learn to play a game like Pente well?
  4. How quickly can such a neural network be trained?
  5. Is there a way to decrease the size of the network needed and decrease the training time needed?

Table of Contents

  1. Introduction
  2. Data Gathering, Cleaning, and Prep
  3. Training a Neural Network to Estimate Win Probability
  4. Conclusion

Comments

Post a Comment

Popular posts from this blog

Simulating Pente in Python (Data Generation and Labeling)

-
Image
  The goal here is not to try to solve a traditional supervised training neural network task, like image classification or house price regression, so the data collection methods must be different.  Instead of "collecting" data, a game simulation must be used to simulate the game logic behind Pente, and to enable running thousands of games of Pente in only a few minutes.  This has several implications for data cleaning and preparation... mainly, these steps are integrated into the data generation step so they don't need to be done separately later. For those interested, the entire code for the simulator can be interacted with here on Google Colab . Simulating the Game Pente is a fairly easy game to simulate because the win conditions and rules are both simple.  Legal moves are simply determined by whether a board position is occupied or not, and finding unoccupied positions on the board is not a computationally or conceptually difficult process.  Then, out o...
Read more

Training a Neural Network to Estimate Win Probability

-
Image
 Data Prep Visualization Visualizing the entire dataset used for a training iteration is particularly difficult because it is a very large graph.  So instead of visualizing what an actual train/test split looks like, here's an example on a small example graph in figure 1. Figure 1: Example Illustration of Train/Test Split The goal of this figure is to demonstrate that the test dataset is built by randomly selecting about 10% of the nodes from the graph created using MCTS, and then the remaining data is the train dataset. Again, as a reminder, the data contained in each node is the following: Figure 2: Reminder of how our data is stored in nodes An example graph with 10,000+ nodes for reference can be found  here , or you can generate your own dataset using the code here . The large number of features in the dataset (upwards of 700) and the number of nodes in even just a small graph (10,000+) make it particularly difficult to visualize the dataset well.  Figure 1 and ...
Read more